a的x次方泰勒公式展開
泰勒公式(Taylor's formula)是數學中用于在某點附近近似一個可微函數的方法。對于函數 \( f(x) \) 在 \( x = a \) 處的泰勒展開,可以使用以下公式:
\[ f(x) = f(a) + f'(a)(x - a) + \frac{f''(a)}{2!}(x - a)^2 + \frac{f'''(a)}{3!}(x - a)^3 + \cdots + \frac{f^{(n)}(a)}{n!}(x - a)^n + R_n(x) \]
其中 \( f^{(n)}(a) \) 表示函數 \( f(x) \) 在 \( x = a \) 處的第 \( n \) 階導數,\( n! \) 是 \( n \) 的階乘,\( R_n(x) \) 是泰勒公式的余項,表示 \( f(x) \) 和它的泰勒展開式之間的誤差。
對于 \( a^x \) 的泰勒展開,我們通常考慮在 \( x = 0 \) 處的展開,因為 \( a^0 = 1 \) 使得展開更加簡潔。這個函數的泰勒展開式是:
\[ a^x = 1 + x \ln(a) + \frac{x^2 \ln^2(a)}{2!} + \frac{x^3 \ln^3(a)}{3!} + \cdots + \frac{x^n \ln^n(a)}{n!} + R_n(x) \]
這個展開式在 \( |x| < 1 \) 時收斂。
如果你需要在其他點 \( x = b \) 處的展開,或者需要更詳細的展開式,可以提供更多的信息,我可以幫助你進一步計算。
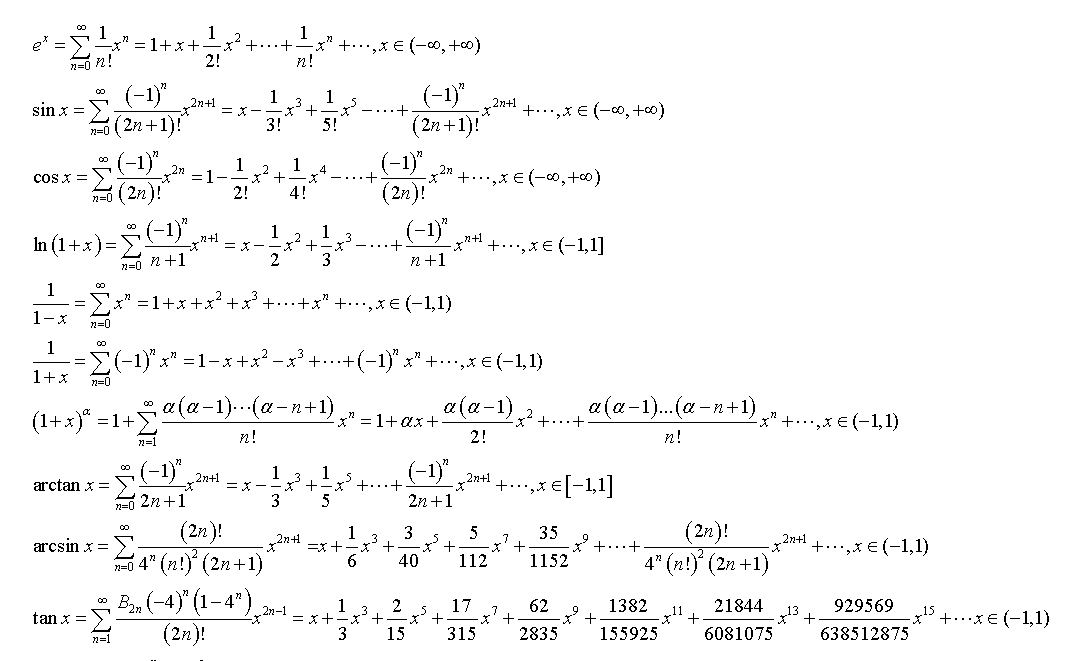
麥勞林公式的使用條件
麥勞林公式(Maclaurin's series)是泰勒公式在 \( x_0 = 0 \) 時的特殊情況,用于將函數展開為無窮級數。使用麥勞林公式需要滿足以下條件:
1. 函數 \( f(x) \) 在 \( x_0 = 0 \) 的某個鄰域內具有所有階的導數。
2. 函數 \( f(x) \) 在 \( x_0 = 0 \) 的鄰域內的泰勒級數(即麥勞林級數)收斂到函數 \( f(x) \) 的值。
3. 余項 \( R_n(x) \) 當 \( n \to \infty \) 時趨向于 0,這是函數能夠展開成級數的充分必要條件。
麥勞林公式的收斂半徑 \( R \) 是一個重要的概念,它決定了級數收斂的區間。收斂半徑可以通過比值測試等方法確定。如果函數 \( f(x) \) 在任一固定點 \( x \) 處的 \( n \) 階導數 \( f^{(n)}(x) \) 有界,則函數 \( f(x) \) 在收斂區間 \( (-R, R) \) 內能展開成麥勞林級數。
在實際應用中,通常需要對于 \( e^x \)、\( \sin x \)、\( \cos x \) 等常見函數,它們的麥勞林級數在整個實數域內收斂,因此可以直接使用其麥勞林公式。而對于其他函數,可能需要先確定其收斂半徑和收斂區間,再決定是否可以展開。
20個常用的泰勒公式展開
泰勒公式是數學中一個非常重要的概念,它允許我們將一個在某點可導的函數展開成無窮級數的形式。下面是一些常用的函數的泰勒公式展開式:
1. \( e^x \) 在 \( x = 0 \) 處的展開:
\[
e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \cdots
\]
2. \( \sin x \) 在 \( x = 0 \) 處的展開:
\[
\sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots
\]
3. \( \cos x \) 在 \( x = 0 \) 處的展開:
\[
\cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots
\]
4. \( \ln(1 + x) \) 在 \( x = 0 \) 處的展開:
\[
\ln(1 + x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \cdots
\]
5. \( \arctan x \) 在 \( x = 0 \) 處的展開:
\[
\arctan x = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \cdots
\]
6. \( \frac{1}{1-x} \) 在 \( x = 0 \) 處的展開(幾何級數):
\[
\frac{1}{1-x} = 1 + x + x^2 + x^3 + \cdots \quad (|x| < 1)
\]
7. \( \sinh x \) 在 \( x = 0 \) 處的展開:
\[
\sinh x = x + \frac{x^3}{3!} + \frac{x^5}{5!} + \frac{x^7}{7!} + \cdots
\]
8. \( \cosh x \) 在 \( x = 0 \) 處的展開:
\[
\cosh x = 1 + \frac{x^2}{2!} + \frac{x^4}{4!} + \frac{x^6}{6!} + \cdots
\]
9. \( \frac{1}{\sqrt{1-x}} \) 在 \( x = 0 \) 處的展開:
\[
\frac{1}{\sqrt{1-x}} = 1 + \frac{x}{2} + \frac{3x^2}{2 \cdot 4} + \frac{5x^3}{2 \cdot 4 \cdot 6} + \cdots \quad (|x| < 1)
\]
10. \( \frac{\sin x}{x} \) 在 \( x = 0 \) 處的展開(利用 \( \sin x \) 的展開):
\[
\frac{\sin x}{x} = 1 - \frac{x^2}{3!} + \frac{x^4}{5!} - \frac{x^6}{7!} + \cdots
\]
11. \( \frac{1}{1+x} \) 在 \( x = 0 \) 處的展開:
\[
\frac{1}{1+x} = 1 - x + x^2 - x^3 + \cdots
\]
12. \( \tan x \) 在 \( x = 0 \) 處的展開:
\[
\tan x = x + \frac{x^3}{3} + \frac{2x^5}{15} + \frac{17x^7}{315} + \cdots
\]
13. \( e^{ax} \) 在 \( x = 0 \) 處的展開:
\[
e^{ax} = 1 + ax + \frac{(ax)^2}{2!} + \frac{(ax)^3}{3!} + \cdots
\]
14. \( \ln(x) \) 在 \( x = 1 \) 處的展開:
\[
\ln(x) = (x-1) - \frac{(x-1)^2}{2} + \frac{(x-1)^3}{3} - \cdots
\]
15. \( (1+x)^\alpha \) 在 \( x = 0 \) 處的展開(二項式定理):
\[
(1+x)^\alpha = 1 + \alpha x + \frac{\alpha(\alpha-1)}{2!} x^2 + \frac{\alpha(\alpha-1)(\alpha-2)}{3!} x^3 + \cdots
\]
16. \( \frac{1}{1-x^2} \) 在 \( x = 0 \) 處的展開(利用 \( \sin x \) 和 \( \cos x \) 的展開):
\[
\frac{1}{1-x^2} = 1 + x^2 + x^4 + x^6 + \cdots \quad (|x| < 1)
\]
17. \( \sec x \) 在 \( x = 0 \) 處的展開:
\[
\sec x = 1 + \frac{x^2}{2!} + \frac{5x^4}{4!} + \frac{61x^6}{6!} + \cdots
\]
18. \( \csc x \) 在 \( x = 0 \) 處的展開:
\[
\csc x = \frac{1}{x} + \frac{x}{6} + \frac{7x^3}{360} + \frac{31x^5}{15120} + \cdots
\]
19. \( \tanh x \) 在 \( x = 0 \) 處的展開:
\[
\tanh x = x - \frac{x^3}{3} + \frac{2x^5}{15} - \frac{17x^7}{315} + \cdots
\]
20. \( \coth x \) 在 \( x = 0 \) 處的展開:
\[
\coth x = \frac{1}{x} + \frac{x}{3} + \frac{x^3}{45} + \frac{2x^5}{945} + \cdots
\]
這些展開式在數學分析、物理學和工程學中都有廣泛的應用。

 微信掃一掃打賞
微信掃一掃打賞